Trong xây dựng các công trình, các kỹ sư xây dựng, kỹ sư tư vấn giám sát thường xuyên phải sử dụng đến tọa độ của các điểm. Dưới đây chúng tôi giới thiệu hai bài toán thuận nghịch cơ bản xác định góc phương vị và chiều dài theo tọa độ của các điểm.
Bài toán thuận xác định tọa độ của các điểm theo chiều dài và góc phương vị
1. Các hệ tọa độ dùng trong xây dựng
Các bản vẽ thiết kế có các giá trị tọa độ X, Y, H. Trong đó tọa độ X và Y xác định vị trí của một điểm trên mặt phẳng. H là độ cao của điểm đó so với một mặt chuẩn nào đó. Mặt chuẩn này có thể là mặt nước biển dùng trong hệ độ cao nhà nước (sea level) nó cũng có thể là mặt đất trung bình của mặt bằng thi công xây dựng (ground level) hoặc độ cao theo mặt phẳng được quy định là (0 của nhà máy hoặc công trình (plan level).
Hiện nay trong xây dựng có hai hệ thống tọa độ được sử dụng đó là: hệ tọa độ độc lập và hệ tọa độ quốc gia.
Hệ tọa độ độc lập (còn gọi là hệ tọa độ qui ước hay hệ tọa độ giả định): Rất tiện lợi nhưng nó chỉ có thể được sử dụng trong một phạm vi hẹp khoảng vài km2 trở lại. Tức là trong khuôn khổ một khu vực đủ nhỏ mà ở đó mặt cầu của trái đất có thể coi là mặt phẳng.
Hệ tọa độ quốc gia: Sử dụng trong các khu vực có quy mô lớn.
2. Khái niệm góc phương vị.
Góc phương vị của một đoạn thẳng là góc theo chiều kim đồng hồ hợp với hướng bắc của hệ trục tọa độ (hoặc đường thẳng song song với nó) và đoạn thẳng đang xét.
3. Bài toán thuận xác định tọa độ của các điểm theo chiều dài và góc phương vị.
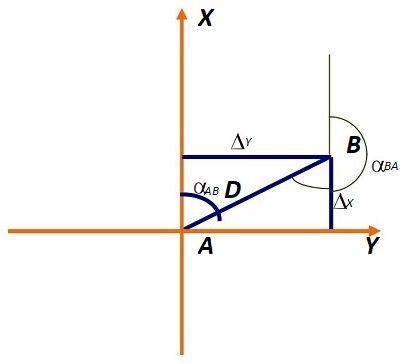
Hình 1- Xác định tọa độ của một điểm
Với đoạn thẳng AB như Hình 1, muốn xác định phương vị của đoạn AB (ký hiệu là (AB) thì từ điểm A ta kẻ một đoạn thẳng song song với trục N và ta có được góc phương vị (AB như hình vẽ.
Giả sử ta đứng tại điểm B nhìn về phía điểm A. Theo quy tắc trên ta sẽ xác định được (BA bằng cách kẻ từ B một đoạn thẳng song song với trục N như cách làm khi xác định phương vị (AB ta sẽ có được góc (BA. Góc (BA gọi là phương vị ngược của (AB.
Từ hình vẽ ta thấy (BA = (AB + 1800 nghĩa là góc phương vị ngược của một cạnh nào đó bằng góc phương vị xuôi của nó cộng thêm 1800.
Giả sử điểm A đã biết trước tọa độ (NA EA), ngoài ra chúng ta cũng biết góc (AB và chiều dài SAB. Theo hình vẽ ta sẽ có:
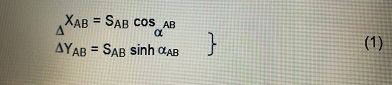
(N và (E là số gia tọa độ của điểm B so với điểm A.
Tọa độ của điểm B sẽ được xác định theo công thức:

Như vậy chúng ta đã xác định được tọa độ của điểm B. Điều kiện cần thiết để xác định được tọa độ là phải biết khoảng cách S và góc phương vị (. Khoảng cách S chúng ta có thể dùng các phương tiện đo chiều dài để đo.
Bài toán nghịch xác định góc phương vị và chiều dài theo tọa độ của các điểm.
Bài toán ngược rất hay được sử dụng để bố trí các điểm từ bản vẽ ra thực tế. Ngoài ra nó còn được sử dụng trong kiểm tra, nghiệm thu công trình .
Từ công thức (1) ta có:

Khi giải bài toán này cần chú ý xét dấu của (N và (E để tránh các sai lầm. Từ hệ trục tọa độ vuông góc và định nghĩa góc phương vị ta có bảng xét dấu như sau:

Các bài toán thuận và nghịch đã được lập trình sẵn cài vào trong các máy tính cầm tay loại kỹ thuật (Scientific calculator). Các kỹ sư tư vấn giám sát, các cán bộ kỹ thuật trên công trường nên mang theo nó ra ngoài hiện trường và cần biết sử dụng thành thạo các chương trình này.